Binary Search Tree JS

So. I’ve tried out a couple of coding tests and one thing I keep seeing is the Binary Search Tree 😰 (“Goes on web hunt”).

I created a simple JS tutorial with an implementation of the Binary Search Tree and some methods based on the knowledge gathered on the web hunt 😼.

A Binary Search Tree is a data structure that stores their objects with the keys in a sorted order so that lookup and other operations use the principle of Binary Search - When adding or looking for a key, traverse the tree from root to leaf, comparing the keys stored in the nodes of the tree and deciding, based on the comparison, whether to continue searching in the left or right subtrees.

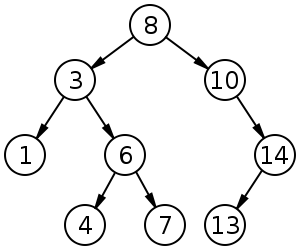
Why Binary Search Tree?

On average, each comparison allows the operations to skip about half the tree, so that each operation takes the time proportional to the logarithm of the number of items stored in the tree. Much better than linear time required to find items by key in an unsorted array, array, but slower than the corresponding operations on hash tables (Which is probably something we’ll be looking at next time).

Create a js file and try these out to see the Binary Search Tree in action! 😬 😎 🤓

Creating a Binary Search Tree

Create a node:

function Node(val) {
    this.value = val
    this.left = null
    this.right = null
}

Create a constructor for the Binary Search Tree:

    function BinarySearchTree() {
        this.root = null
    }

The structure of a Binary Search Tree is as follows:

• Every node value on the left is smaller than the parent node (root)
• Every node value on the right is larger than the parent node (root)

This would require you to find the appropriate location when inserting.

Create the push method to check the node values and insert the value in the correct position:

    BinarySearchTree.prototype.push = function(val) {
        var root = this.root

        if (!root) {
            this.root = new Node(val)
            return
        }

        var currentNode = root
        var newNode = new Node(val)

        while(currentNode) {
            if (val < currentNode.value) {
                if(!currentNode.left) {
                    currentNode.left = newNode
                    break
                } else {
                    currentNode = currentNode.left
                }
            } else {
                if (!currentNode.right) {
                    currentNode.right = newNode
                    break
                } else {
                    currentNode = currentNode.right
                }
            }
        }
    }

Once you have that, you can now create an instance of a Binary Search Tree and push values to it! 😃

Create an instance:

    var bst  = new BinarySearchTree()

Push some values:

    bst.push(40)
    bst.push(25)
    bst.push(10)
    bst.push(32)
    bst.push(78)

Now lets create some methods to traverse the tree and get the minimum and maximum values 😊

Pre Order Traversal

Traverses the tree from the parent node and visits the left side of the tree, left subtree-first, then proceeds to the right subtree.

So the values after the pre order traversal would correspond to: 40, 25, 10, 32, 78

    function preOrder(node) {
        if (node) {
            console.log(node.value)
            preOrder(node.left)
            preOrder(node.right)
        }
    }

In Order Traversal

Traverses the tree from the deepest left subtree, in order from smallest to largest value.

So the values after the in order traversal would correspond to: 10, 25, 32, 40, 78

    function inOrder(node) {
        if (node) {
            inOrder(node.left)
            console.log(node.value)
            inOrder(node.right)
        }
    }

Post Order Traversal

Traverses the deepest levels of the subtrees, left to right of the subtree, eventually reaching the parent node.

So the values after the post order traversal would correspond to: 10, 32, 25, 78, 40

    function postOrder(node) {
        if (node) {
            postOrder(node.left)
            postOrder(node.right)
            console.log(node.value)
        }
    }

Now lets call all the above methods and log a nice message above each one so we know which results we’re looking at!

    console.log("Pre order traversal: ");
    preOrder(bst.root)

    console.log("\nIn order traversal: ");
    inOrder(bst.root)

    console.log("\nPost order traversal: ");
    postOrder(bst.root)

Sweet! The values log as expected. Now let’s create some methods to get the minimum and maximum values form the tree.

Min Value

Gets the smallest value from the tree: 10

    function minNode(node) {
        if (!node) {
            return 0
        }
        if (node.left) {
            return minNode(node.left)
        }
        return node.value
    }

Max Value

Gets the maximum value from the tree: 78

    function maxNode(node) {
        if (!node) {
            return 0
        }
        if (node.right) {
            return maxNode(node.right)
        }
        return node.value
    }

Lets log the minimum and maximum values:

    console.log("\nMin Value: ");
    console.log(minNode(bst.root));

    console.log("\nMax Value: ");
    console.log(maxNode(bst.root));

Awesome! 😬 😬 😬

I hope this cleared the air about Binary Search Tree’s in even the slightest bit!

Check the Github repo for this tutorial:

• Binary Search Tree in JS

Check these out for some further reading (It’s what the tutorial is based off of):

• Rosetta Code: Tree Traversal

• JS: Binary Search Tree

• Wikipedia: Binary Search Tree

Happy Coding!!! 👽 🤓 👾